Income distribution

Monte Carlo simulation
economics
Published

March 27, 2025

A BBC report dated 16th January 2023 presents an interesting statistics. It quotes an OXFAM report, stating that 40% wealth is in the hands of top 1%.

This can be taken as 40:1 Pareto index.

Figure 1: Income distribution as seen by Pareto

What is Pareto index?

Italian polymath Vilfredo Pareto observed that approximately 80% of Italy’s land was owned by 20% of the population. It is surprisingly self similar over a wide range of magnitudes. That means, 20% of the 20% of total population own 80% of 80% of total land and goes on.

Income distribution is not normal

Hence the outcomes completely differ from Normal or Gaussian distribution.

This is a simplification of a general rule. The ratio or index can be any where and need not add up to 100.

Parameters of Pareto distribution

The Pareto distribution can be described with only 2 simple parameters, ⍺ and xm.

Calculating the 𝛂

If the Pareto ratio is x:y,

\[𝛼 = log(x+y)/log(x)\]

Exact formula is logx(x+y)

Here, \[𝛼=log(41)/log(40)\]

⍺ = 1.0067

Smaller the ⍺, the larger the proportion of very high-income people and vice verse. Here we can that the index is very low, close to 1.

xm

It is the minimum value of the parameter under study.

Case Scenario

Assume that a marginal individual works for 308 days a year with a minimum wage of ₹105. Her yearly income will be around ₹32400. This can be taken as the minimum value of x, the income distribution we are studying. Let’s call it xm.

What will be the mean and median income of the community in which she is living? What will be the maximum income possible? Let’s calculate

Monte Carlo simulation of income distribution

Monte Carlo Simulation can be defined as a computational method of repeated random sampling to obtain numerical results. It can be done using excel with or without add-ons for simulation. Excel does not natively support Pareto sampling. Free Open Sourse add-ons like XLRisk also (right now) does not support the same. r is excellent tool in this situation and also for Monte Carlo simulation of returns for volatile instruments using levi stable distribution

r for simulating income distribution

First, install the necessary package VGAM if you haven’t already and load.

Code 
library(VGAM)

Choose the parameters for the Pareto distribution. We have already calculated the ⍺ and xm. See Section 3

Code 
alpha <- 1.0067
xm <- 32400

Use the rpareto function to generate random samples. Let’s simulate the wealth of 1000 individuals.

Code 
n <- 10000  # Number of individuals
income_samples <- rpareto(n, scale = xm, shape = alpha)

To perform a Monte Carlo simulation, we will repeat the random sampling multiple times and analyze the results. Let’s say we want to perform 10000 simulations.

The simulation1

Code 
num_simulations <- 10000
simulation_results <- matrix(NA, nrow = num_simulations, ncol = n)

for (i in 1:num_simulations) {
  simulation_results[i, ] <- rpareto(n, scale = xm, shape = alpha)
}

# Summarize the results
mean_income <- apply(simulation_results, 1, mean)
median_income <- apply(simulation_results, 1, median)
sd_income <- apply(simulation_results, 1, sd)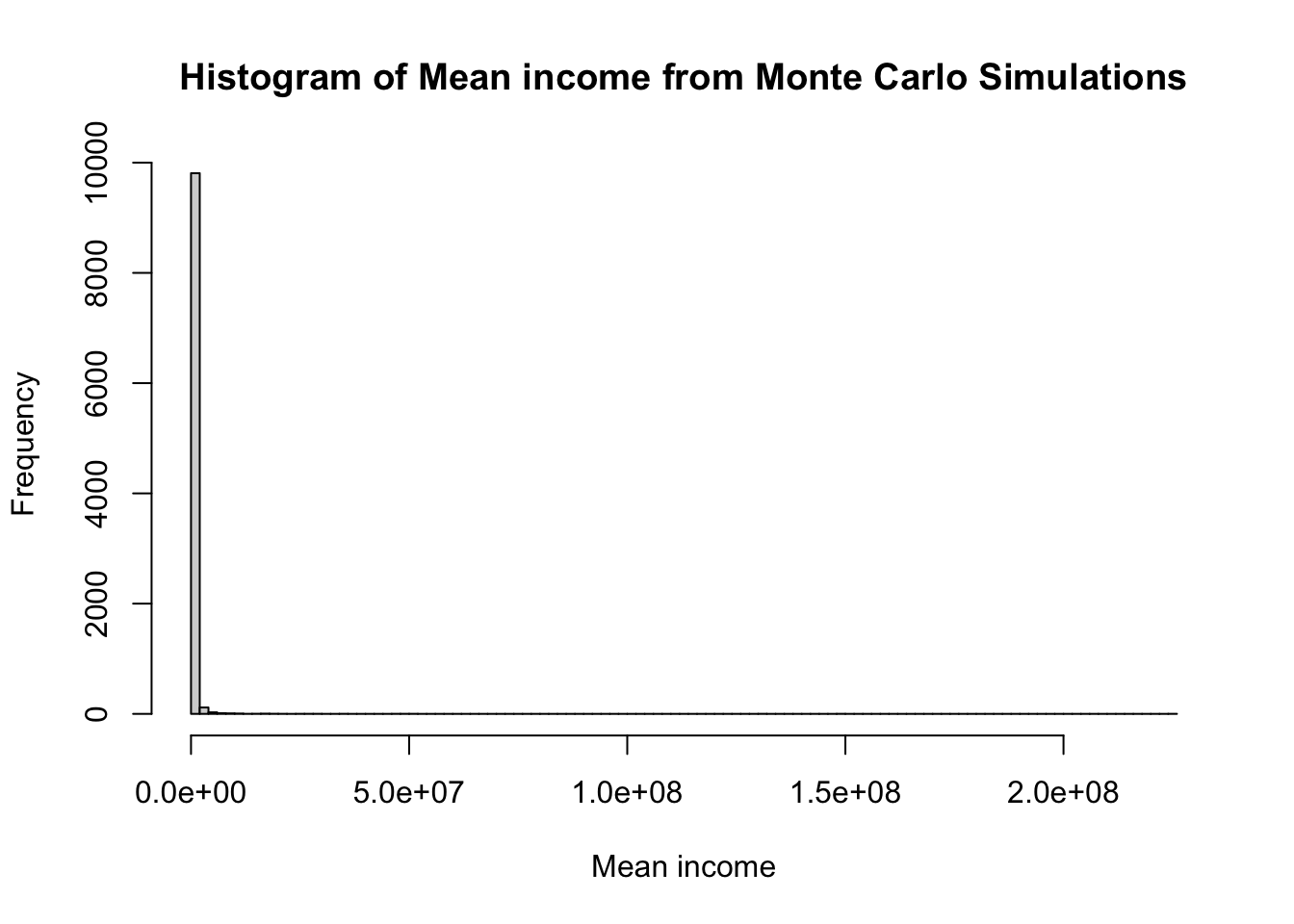

Visualisation of mean income

Code 
# Histogram of mean income from simulations
hist(mean_income, breaks = 125, main = "Histogram of Mean income from Monte Carlo Simulations", xlab = "Mean income")

Code 
# Summary statistics
summary(mean_income)
     Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
   210536    297412    346174    564802    441032 224754083
Code 
summary(median_income)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  61914   64069   64492   64496   64920   67486
Code 
summary(sd_income)
     Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
9.373e+05 3.391e+06 5.787e+06 2.690e+07 1.229e+07 2.242e+10

Distribution of median income

Median income is the most likely income one can expect in this community. It is an approximation of geometric mean of all the possible incomes.

Code 
# Density plot of median income
plot(density(median_income), main = "Density Plot of Median income", xlab = "Median income")

Visualisation of the paths

# Generate colors for the paths
colors <- rainbow(num_simulations)

# Plot the first simulated path with the first color
plot(1:n, simulation_results[1, ], type = "l", ylim = c(min(simulation_results), max(simulation_results)),
     xlab = "Individual", ylab = "Income", main = "Simulated Paths of Income", col = colors[1], lwd = 2)

# Add the rest of the simulated paths with different colors

for (i in 2:num_simulations) {
  lines(1:n, simulation_results[i, ], col = colors[i], lwd = 2)

Interpretation

  • Mean income:
    • The minimum mean income observed across simulations is ₹210,665.
    • The first quartile (25th percentile) of mean income is ₹296,141, indicating that 25% of simulations have mean income below this value.
    • The median mean income is ₹342,900, which represents the middle value of the distribution.
    • The mean mean income across all simulations is ₹585,468.
    • The third quartile (75th percentile) of mean income is ₹437,320, indicating that 75% of simulations have mean income below this value.
    • The maximum mean income observed is ₹372,658,431.
  • Median income:
    • The minimum median income observed across simulations is ₹62,016.
    • The first quartile (25th percentile) of median income is ₹64,076, indicating that 25% of simulations have median income below this value.
    • The median median income is ₹64,504, which represents the middle value of the distribution.
    • The mean median income across all simulations is ₹64,513.
    • The third quartile (75th percentile) of median income is ₹64,941, indicating that 75% of simulations have median income below this value.
    • The maximum median income observed is ₹66,950.
  • Standard Deviation of income:

    • The minimum standard deviation of income observed across simulations is ₹883,000.

    • The first quartile (25th percentile) of standard deviation of income is ₹3,341,000, indicating that 25% of simulations have standard deviation of income below this value.

    • The median standard deviation of income is ₹5,665,000, which represents the middle value of the distribution.

    • The mean standard deviation of income across all simulations is ₹29,140,000.

    • The third quartile (75th percentile) of standard deviation of income is ₹11,940,000, indicating that 75% of simulations have standard deviation of income below this value.

    • The maximum standard deviation of income observed is ₹37,240,000,000.

Summary

While the marginal worker is earning ₹2700 per month, the minimum mean income per month for the community is 17500 per month. i.e, the lowest observed mean of the simulations. Similarly, the maximum mean income is ₹3.1Cr.

Median income is around ₹5375.

These summary statistics provide insights into the asymmetry of income distribution and variability of income across the simulated scenarios. Let’s have a final look at Income distribution.

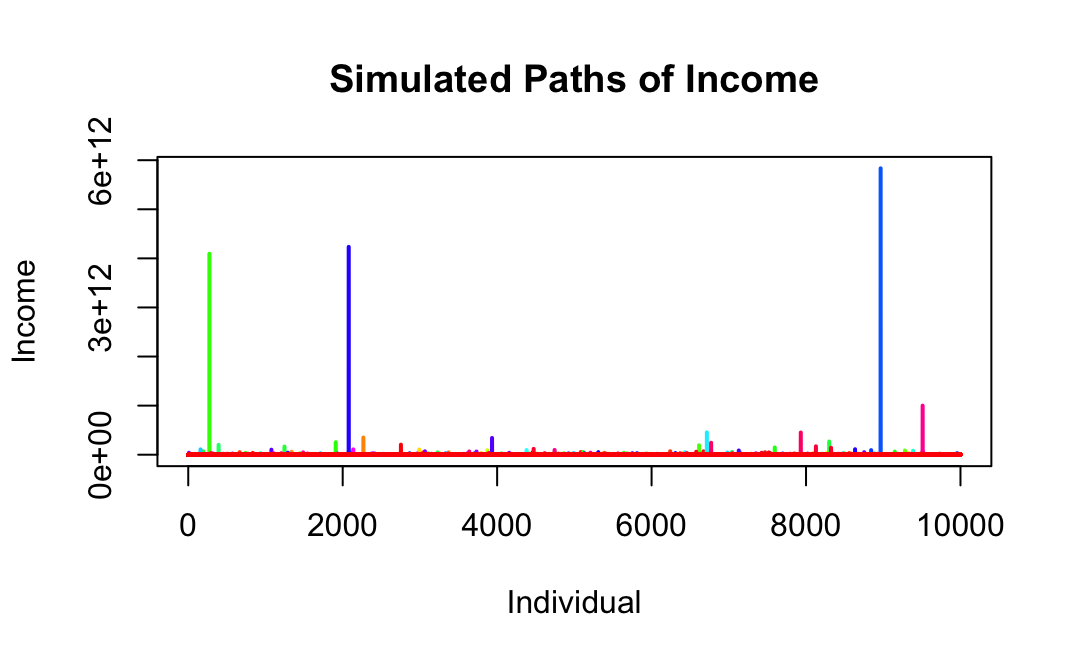
The individual incomes of many, represented by the red lines, languish in the shadows of colossal giants. These titanic paths of income towering above, dwarfing the humble incomes below, paints a stark contrast between the vital few and the useful many.

We can make another important inference from this analysis:

Any meaningful and organic improvement in the xm, that is the minimum value of x, (the minimum wage here) will exponentially increase the total wealth of the community.

Back to top

Footnotes

  1. Explanation of the code

    • NA: This specifies the value that will fill the matrix. In this case, NA indicates that each element of the matrix will be initialized as a missing value.

    • nrow = num_simulations: This argument specifies the number of rows in the matrix. Here, num_simulations is the number of simulations we want to run, so the matrix will have num_simulations rows.

    • ncol = n: This argument specifies the number of columns in the matrix. In our code, n is the number of individuals we want to simulate wealth for, so the matrix will have n columns.

    • for (i in 1:num_simulations): This loop iterates num_simulations times, where i takes on the values from 1 to num_simulations.

    • simulation_results[i, ] <- rpareto(n, scale = xm, shape = alpha): In each iteration of the loop, you’re generating a set of random wealth values for n individuals using the Pareto distribution specified by the parameters scale = xm and shape = alpha.

    • rpareto(n, scale = xm, shape = alpha): This function generates n random numbers from a Pareto distribution with scale xm and shape alpha.

    • simulation_results[i, ] <- ...: This assigns the generated random wealth values to the i-th row of the simulation_results matrix. Each row of simulation_results represents the wealth distribution for one simulation iteration.

    ↩︎